É possível prever o futuro?

Certa vez um aluno do curso de ciências atuárias me perguntou como “prever” os valores futuros de uma série temporal. Ele estava interessado especificamente nas cotações de ações negociadas na Bolsa de Valores e de outros “ativos” exóticos como, por exemplo, Bitcoin, Ethereum e Litecoin  negociados em outras exchanges.

A pergunta do aluno, ilustrada na figura 1 abaixo, pode ser estendida para outras áreas como climatologia (p. ex., a previsão da temperatura ou do degelo no Ártico), epidemiologia (p. ex., a previsão do número de pessoas que irão contrair o vírus influenza no próximo verão), criminologia (p. ex., a previsão do número de pessoas assassinadas no próximo mês), jurimetria (p. ex., a previsão do número de processos de um determinado tipo), economia (p. ex., a previsão do PIB ou da inflação para o próximo ano), entre outras.

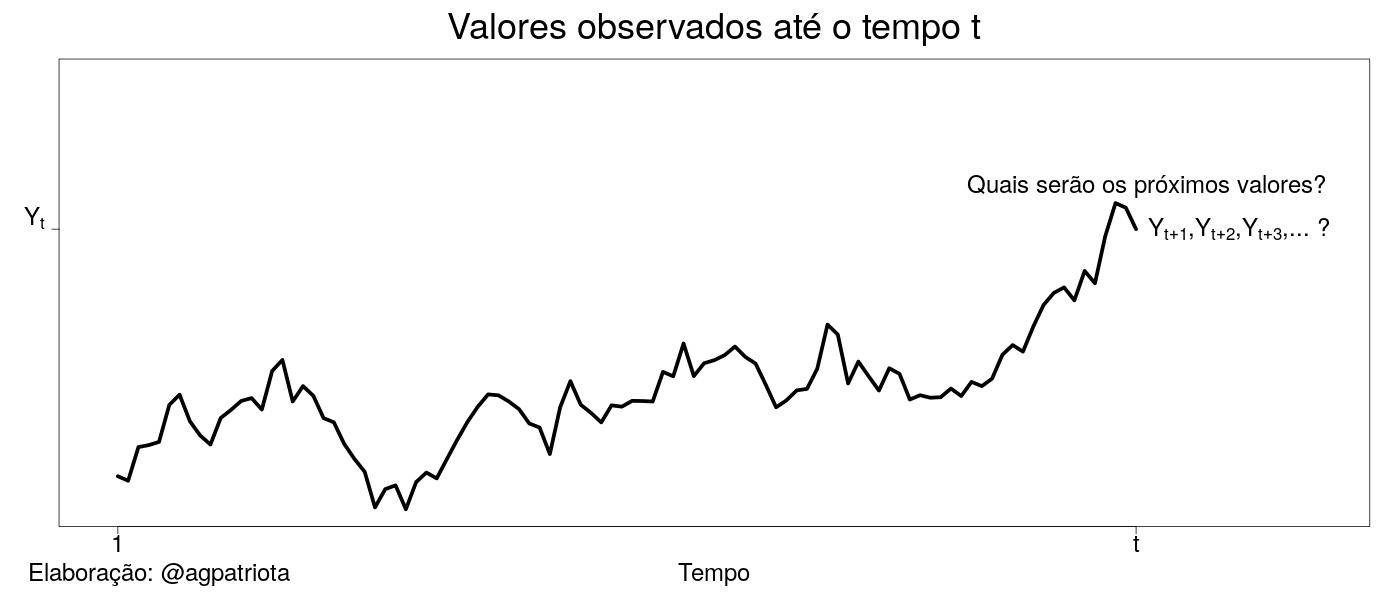
Felizmente, a teoria estatística é desenvolvida de uma forma geral permitindo que várias áreas possam utilizar a mesma metodologia para resolver problemas diferentes. O tema específico de previsão de valores futuros está inserido em uma disciplina da Estatística chamada de séries temporais.

As séries temporais, em especial, têm a seguinte característica fundamental: um valor futuro depende fortemente do que aconteceu em seu histórico passado. Isso indica que a análise estatística deve ser condicional às observações que ocorreram em períodos anteriores.

No que segue, apresento informalmente o procedimento estatístico utilizado para calcular probabilidades para os valores futuros Y_t+1, Y_t+2, Y_t+3 dado que observamos o passado Y₁, Y₂,…, Y_t,  por meio do modelo mais simples, a saber,

em que "e_t" é o erro do modelo, também conhecido como ruído branco¹. Basicamente o modelo está dizendo que a diferença entre um valor presente e o do seu passado imediatamente anterior, ou seja, Y_t  - Y_t-1, não contém informação relevante sobre a tendência da série. Sob esta suposição, podemos calcular a probabilidade de um valor futuro estar em um determinado intervalo.

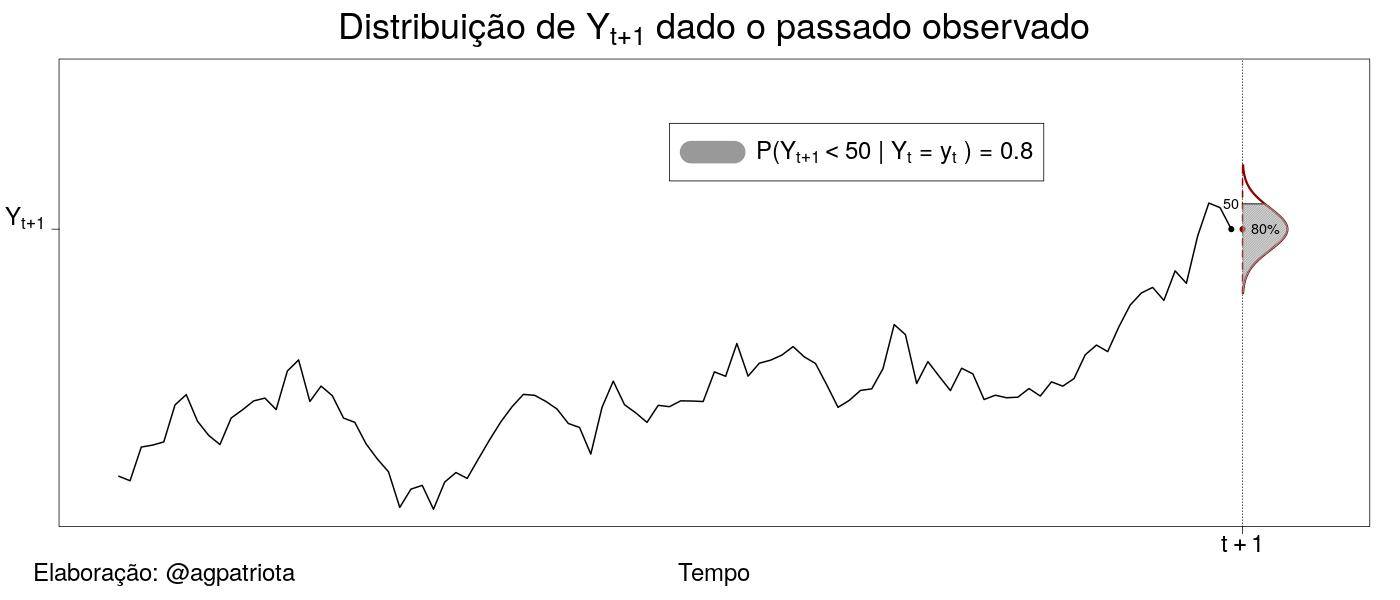
A figura 2 ilustra a distribuição de probabilidades de um valor futuro Y_t+1 dado o histórico observado. No caso ilustrado na figura 2, a probabilidade de Y_t+1 ser menor do que 50 (unidades de medida) dado todo o histórico² foi estimada ser 80%. Com essa informação o analista pode tomar uma decisão. A curva vermelha destacada na vertical para o ponto no tempo t+1 é a função densidade de probabilidade³ da variável em um futuro próximo (t+1) dado todo o histórico observado. A partir dela, o estatístico consegue calcular probabilidades e intervalos de confiança para o valor futuro. Com essas informações o analista pode tomar alguma decisão importante como, por exemplo, vender o ativo no preço atual ou comprar mais.

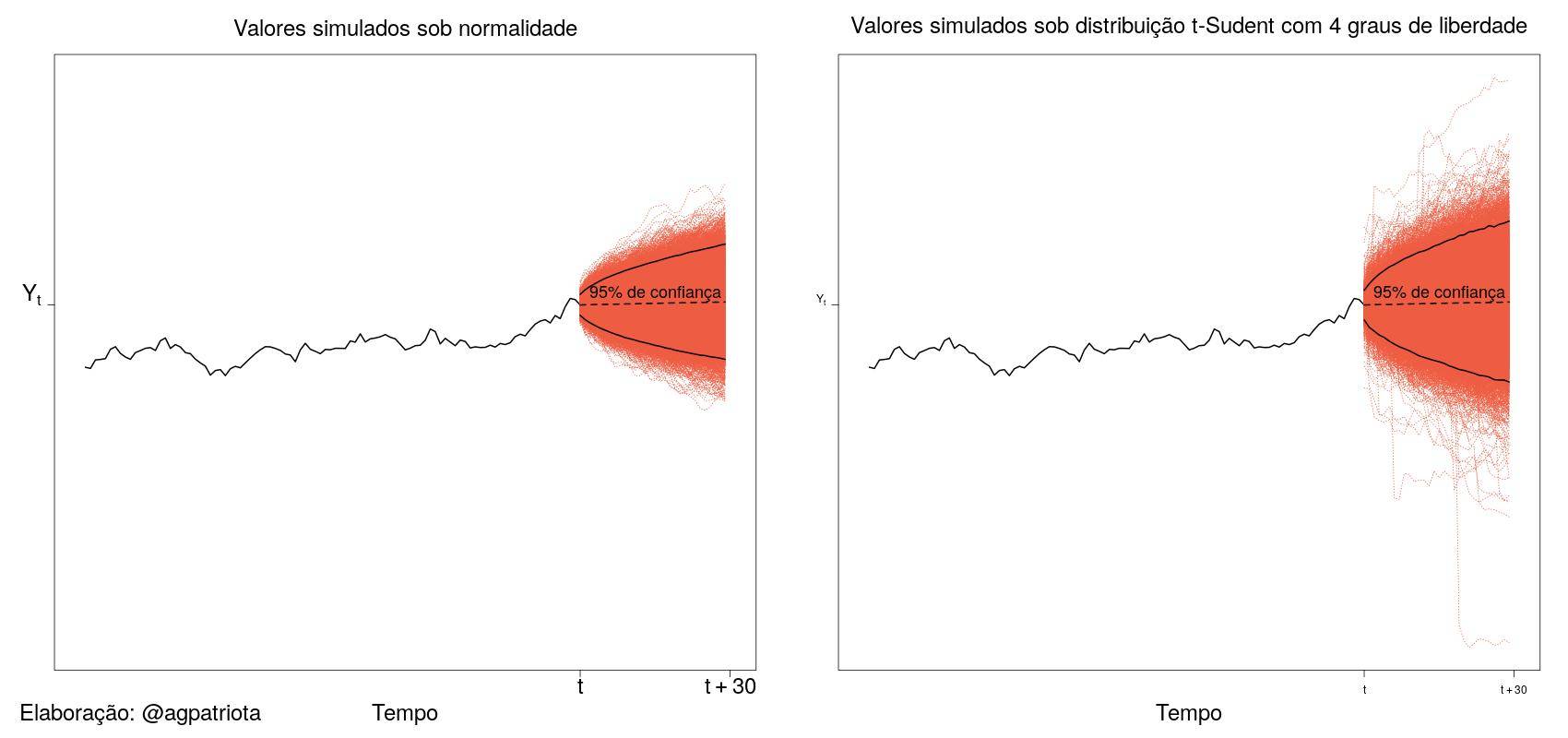
É possível calcular probabilidades para tempos futuros t+2, t+3 e assim por diante. No entanto, a distribuição de probabilidades em tempos futuros mais distantes tenderá a abrir o leque para mais possibilidades, pois um futuro mais distante é mais incerto do que um futuro imediato (veja a figura 3).

A Figura 3 apresenta valores futuros simulados e intervalos de previsão com 95% de confiança considerando duas distribuições para o erro do modelo, a saber, distribuição normal e distribuição t-Student com 4 graus de liberdade. A primeira é mais sensível a valores atípicos (distantes da média). A segunda tem caudas mais pesadas e portanto é mais robusta para modelar valores distantes da média.

Espera-se que 5% dos valores futuros sejam observados fora das bandas de confiança. Quanto mais variabilidade, mais largas serão as bandas de confiança. Além disso, observe que as bandas de confiança sob a distribuição t-Student são mais largas do que as obtidas sob normalidade. Isso é esperado para comportar os valores atípicos dentro das bandas.

Problemas

Os métodos estatísticos não fazem mágica. Um dos grandes problemas é o de assegurar que o modelo utilizado seja adequado para o problema em questão. Se um modelo inadequado for utilizado, as probabilidades e bandas de confiança calculadas poderão sustentar decisões equivocadas. Há formas de validar o modelo por meio de análise de resíduos e estudos de simulação. Entretanto, poucos trabalhos que fazem uso dos métodos estatísticos empregam sistematicamente essas técnicas de validação, o que imprime uma certa desconfiança aos resultados obtidos.

Antes de definir alguma política de ação, baseando-se nas figuras 2 e 3 ou em qualquer outra técnica estatística, o analista deve validar o modelo escolhido por meio de diversas técnicas de validação que estão disponíveis na literatura estatística (análise de resíduos, análise de influência local e global, análise de sensibilidade do modelo, verificação das suposições sobre o erro, entre outras). Ao ler um artigo, certifique-se de que o autor validou o modelo e busque saber quais as técnicas foram utilizadas.

Em algumas áreas, por exemplo em climatologia e economia, um problema adicional ocorre: alguns valores do histórico passado não são observados diretamente e o analista precisa utilizar alguma técnica estatística⁴ para “adivinhar” os valores da série não observados. Isso embute mais variabilidade no processo e as bandas de confiança tenderiam a ficar mais largas, aumentando assim a incerteza das observações futuras. Caso essa variabilidade não seja levada em conta, as probabilidades e bandas de confiança calculadas não serão confiáveis.

Caso o leitor se interesse em aprofundar os estudos nesse assunto, veja a lista de referências abaixo.

Referências

• Fuller, W.A. (1996). The Statistical Analysis of Time Series. Second Edition. Wiley.
• Hamilton, J. (1994). Time Series. Princeton University Press.
• Morettin, P.A. and Toloi, C.M.C. (2006). Análise de Séries Temporais, Segunda Edição. Blucher.
• Shumway, R.H. (1988). Applied time series analysis. Pretice-Hall.
• Shumway, R.H. and Stoffer, D.S. (2010). Time Series Analysis and Its Applications. Third Edition, Springer.
• Taylor, S. (2008). Modelling Financial Time Series, 2nd Ed. Wiley.

Alexandre Galvão Patriota é professor livre-docente de estatística no Departamento de Estatística do Instituto de Matemática e Estatística da Universidade de São Paulo.

Notas de rodapé:

¹ No ruído branco, estão todas as informações que não foram explicitadas no modelo. Se há informação relevante que explique a variabilidade de Y_t mas não tenha sido explicitada no modelo (o modelo acima não explicita informação alguma que não seja o passado imediato de Y_t), então a previsão será menos precisa do que aquela obtida de modelo que considerasse a informação relevante.

² Pode-se também calcular a probabilidade de Y_t+1 ser maior do que 20 (unidades de medida) ou estar em qualquer intervalo real dado todo o histórico.

³ A função densidade de probabilidade é um conceito importante estudado em disciplinas básicas de estatística. A área abaixo da curva em um determinado intervalo é a probabilidade de a variável estar nesse intervalo.

⁴ Os métodos de imputação de dados são utilizados para “adivinhar” o valor do dado faltante por meio de variáveis auxiliares chamadas de proxies.